It is a very common situation when we work with signals coming from various sensors (anything from microphone to blood pulse detector) - there is some noise or other unwanted features in the signal - and we want to get rid of them.

Typically this "get rid" means that such features have different frequency from the main signal. And luckily, there are methods which allow to reduce any signal components according to their frequencies.

These methods are called "digital filters". There may be also "analog filters" - i.e. implementations in form of some electronics etc - but digital ones are nice as they can be changed without physical changes.

One of the general classifications divides filters according to what ranges of frequencies they affect. I.e. there are:

• low-pass filters (LPF) which don't affect frequencies below some F0 but reduce anything higher (imaging clearing voice record of various environmental hisses)
• high-pass filters (HPF) which on contrast reduce everything below some corner F0 value and leave anything higher as is (for example it's crucial for IR-sensors of TV remote control to remove any slow changes caused by changing of ambient light)
• band-pass filters (BPF) which reduce anything higher or lower than our wanted range (or band) of frequencies, usually around some center frequency F0.

Note that both BPF and HPF will also effectively cancel any constant component of the signal (which corresponds to zero frequency) so their output has average close to zero even if the input is biased.

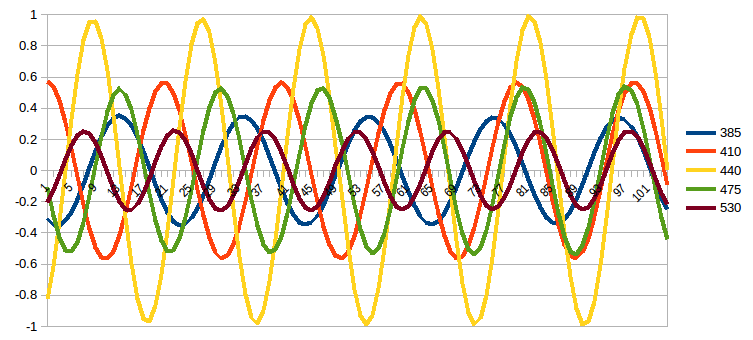
Here "reducing" don't happen steeply. Rather some intermediate frequencies are reduced slightly and others. The picture below shows how "narrow" band-pass filter tuned to 440Hz affects neighboring frequencies. All 5 waves have amplitued of 1.0 at input, but 385Hz and 530Hz are reduced more to below 40% while closer 410Hz and 475Hz keep slightly below 60% of their original swing (while "central" frequency is unchanged at all).

Implementation details

Now, what algorithm is behind these filters? It is quite simple to write (though not as simple to explain)!

Imagine, that we got our signal as the indexed sequence (like array) X and denote its values as x[n] (current), x[n-1] (previous), x[n-2] (for one before previous) etc.

We want to build along it another sequence Y, indexed in the same manner.

Now the "filter" is just the formula which allows to calculate new value y[n] based upon the current (and few previous) values of x and, probably, few previous values of y.

One of the simplest examples, we probably already may meet somewhere, is the average of two (or several) last input values:

y[n] = (x[n] + x[n-1]) / 2

Even more smooth "averaging" is created by taking previous y instead of previous x (this creates analog of "feedback" in physical system):

y[n] = (x[n] + y[n-1]) / 2

And we can also assign different weights to components (instead of 1/2 for both), like this:

y[n] = x[n]/4 + y[n-1])*3/4

or even

y[n] = x[n]/4 + y[n-1])/4 + y[n-2]/4 + y[n-3]/4

Which will make our filter to react even more slowly to changes of input signal and produce even more smooth output.

All these "averaging" filters are examples of LPF by the way. But now try to guess what the filter we get if we subtract "filtered average" (produced by one of these) from the current value? It would be on contrary something like HPF, which will only show sudden changes of signal but then will return to average zero...

General form

So digital filters are often represented by formula including several components from both x and y with some coefficients. In symmetric way it could be written like this:

y[n]*a0 + y[n-1]*a1 + y[n-2]*a2 + ...  =  x[n]*b0 + x[n-1]*b1 + x[n-2]*b2 + ...

Or if we rewrite it leaving only unknown y[n] on the left:

y[n] = (x[n]*b0 + x[n-1]*b1 + x[n-2]*b2 + ... - y[n-1]*a1 - y[n-2]*a2 - ...) / a0

And the whole magic works like this:

• find out necessary coefficients a0, a1, a2..., b0, b1, b2... for wanted filter type
• set few initial values of y to anything (e.g. zero)
• continue calculating values of y using the formula above, with each new value of x

The secret of chosing good coefficients is where real magic (and deep math) happens. Specific methods are sometimes named after scientist who invented them (e.g. "Butterworth" or "Chebyshev" filters).

However we usually need not reinvent the wheel and use some "recipe" to calculate coefficients for specific type of filter.

Coefficient recipes

One of the popular sources for several general forms of filters is the document titled "Cookbook formulae for audio EQ biquad filter coefficients" by Robert Bristow-Johnson. It could be googled easily on internet. You may also use the preserved reference copy I've uploaded to github (to prevent broken links).

Look at "Equation 4" there - it is just our filter formula with two preceeding values of X and two of Y, also taking into account current value of X. It is often called Biquad filter as in symmetric form both parts form a kind of quadratic equation.

Now we want BPF recipe from this cookbook. There are two of them (closer to end of text) - let's choose one with "0 db peak gain" - i.e. not reducing or amplifying the center frequency. This recipe expressess b0, b1, b2, a0, a1, a2 coefficients via alpha and w0 intermediate variables.

Look higher in the text to find out that

w0 = 2*pi*f0/Fs
alpha = sin(w0)/(2*Q)

Here Fs is the "sampling frequency" - i.e. how many samples per second our signal contains. F0 is the center frequency for which we care (i.e center of the band). Magical component Q is the quality factor of the filter - it simply describes how "narrow" the filtered band should be. You can read more about it and select it thoughtfully - or just play with few values to find out a suitable one.