The idea for this problem was suggested by Laurent Petit in this topic - Thanks a lot!
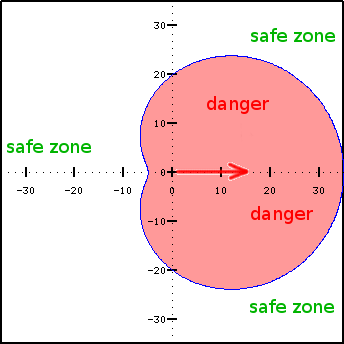
In the first part of Lord of the Rings there is a blood-chilling scene when Frodo and his companion hobbits are overtaken by the Black Riders in the road and save themselves by hiding in the forest growing by the sides of the road.
Now imagine there is a square area (a part of the forest for example) with dimensions 100*100 yards
with several Black Riders in it, trying to find poor hobbits.
Each Black Rider has a limited field of view, as shown in the picture above. Suppose the Rider is standing
at the point (0,0) and looking along the X axis (red arrow). f course he can see futhest straight ahead,
but has limited perception of what is happening behind him (relying on non-visual feelings). The boundary of this
field of view is described by simple equation in polar coordinates:
R = 20 + 15 * cos(theta)
where the theta is an angle between the direction to the given point (e.g. some hobbit) and
the direction in which the Rider is currently facing.
For example, if the Rider is looking along Y axis (i.e. his look direction is pi/2) and the hobbit is at
position (30,30) - he is safe, but if he is at position (10,10) the Rider will discover the poor fellow.
Angles are in radians and calculated in CCW direction from the X axis. The field has coordinates
(0,0) at one corner and (100, 100) at the other.
Your goal is to evaluate roughly, what percentage of the field is "visible" to what number of riders. I.e. how many and how safe space there still exist.
Input data will give N - the amount of riders (4..6) in the first line.
Next lines will contain X, Y and angle (looking direction) for each of riders.
Answer should contain N+1 values - first of them specifying percentage of the field not covered by any
rider, next one describing how many percents are visible to any single rider, then percentage for space guarded
by two riders simultaneously and so on. All these values should be rounded to integer (and you need not worry
if the sum is not exactly 100% due to rounding).
Example:
input data:
4
20 81 0.6
39 35 0.5
90 16 -1.5
85 20 -1
answer:
63 31 7 0 0
In this example 63% of the area are safe, 31% is guarded by any single rider and 7% are guarded by some
pair of riders simultaneously.