Neural Network Calculation

If you are completely ignorant about Artificial Neural Networks, feel free to browse intro.

Let's learn how Neural Network (or NN) is built of Neurons, and how we calculate values (or signals) propagating from its inputs to outputs.

Neurons

Basically, Neural Network is a "net" of Neurons. As programmers, we can say it is a graph in which Neurons are nodes. And what is a Neuron?

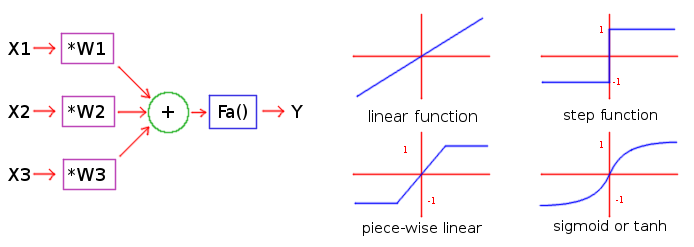
Neuron is a small thing which takes several values and produces result:

• in basic form neuron simply sums up its input values
• it also contains weight coefficients by which input values are multiplied so some inputs may have greater effect on result and others smaller effect
• result may be limited by some function (called activation function) to fit into some range, say (-1.0 ... 1.0)

Look at the picture above (left) for visual interpretation of how inputs are multiplied by weights, added to make total - and this total is passed through activation function. We can also describe this with simple formula (where Y is result and Xs are input values):

Xsum  =  X1 * W1 + X2 * W2 + ... + Xn * Wn

Y  =  Fa(Xsum)

Looks clear, right? Except, what is an activation function? In simplest form we may go without it (Y = Xsum), but it is inconvenient. Suppose all inputs and weights are in range -1.0 ... 1.0 - but their sum won't fit this range! Since the result may be used as input for further neurons, we often want to limit it. We can divide it by the number of input values (this gives "linear function" Y = Xsum / n), or we can hard-truncate it if coming out of range, e.g. Y = min(max(Xsum, -1), 1) - this shall be called "piece-wise" linear function.

We shall use similar but smooth function called "sigmoid", with original forumla Y = 1 / (1 + exp(-Xsum)). However in this form it has output range 0 ... 1, so let us multiply it by 2 and subtract 1, so it is stretched vertically twice and shifted down to cross the origin:

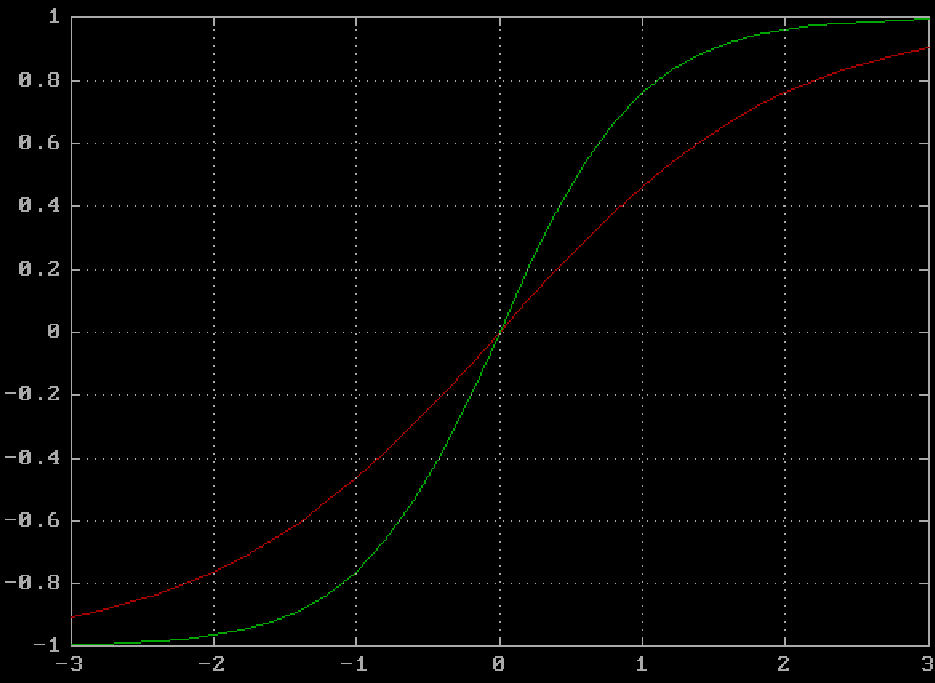
Y  =  2 / (1 + exp(-Xsum * Ks)) - 1

Here we also add "sharpness" coefficient Ks, let normally have it 2. In the chart below red line is with Ks = 1 and green with Ks = 2. With 2 you may see that in the middle range -0.5 ... 0.5 the function is very close to "identity" (Y = Xsum). This doesn't affect performance of the network but may be convenient in manual analysis.

Topology

So how neurons are connected into the network? It is directed graph - meaning that input signals travel (propagate) further and further to output. Topology (i.e. shape) of the network could vary greatly (and it is a matter of separate study), but often we use simple idea: network consisting of layers:

• there are several layers (say, 3 or more)
• every layer contains several neurons
• layers are ordered, the very first layer is input layer, the last is output layer and between them several inner (or hidden layers) are sandwiched
• every neuron takes as its inputs all results from previous layer
• input layer doesn't have inputs, rather its "results" are assigned manually (they are inputs to network)

Any such topology could be uniquely described by sequence of numbers - counts of neurons in each layer. For example 3-2-1 means 3 neurons in input layer, 2 in single hidden layer and 1 in output layer. Below are visualisations of couple more topologies:

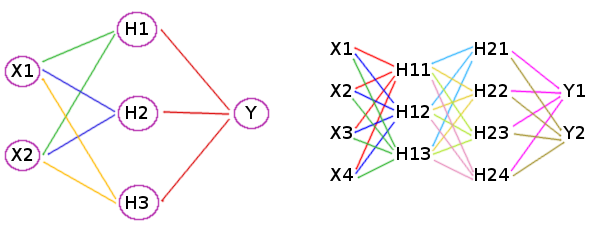
The left network has topology 2-3-1, with neurons of hidden layers marked as H1 ... H3. Here green lines are inputs to H1 neuron, blue are inputs to H2, yellow are inputs to H3 and red are inputs to Y - the only output neuron.

The second picture gives neural network with two hidden layers, so the neurons in them are marked with two digits. Also it has two outputs. Its topology is 4-3-4-2.

Calculation

At this point we know enough to calculate neural network! We understand that the network is defined by its topology and all the weights on every neiron input. Topology is generally preset by the creator of the network, but weight coefficients are set up during process called "training".

We shall learn how to train the neural network in the following problem. For now let's just calculate it with some given inputs and weights, to make sure we can arrange our mathematics properly.

1. We are given topology of the network and all the weight coefficients.
2. Also we are given input values - assign them to neurons of the input layer.
3. Calculate results for first hidden layer, then next one and so on - at last calculate output layer.
4. Print the result - that's all!

Input data contain topology in the first line (space separated counts of neurons in each layer, from input to output)
Next lines contain weights on inputs for every neuron of every layer except first
Remaining lines contain sample inputs (one test-case per line), preceded by line with single value - number of the following test-cases.

Answer should give outputs for each test-case - outputs are space-separated and values in them are also space-separated (but as we know number of outputs there is no confusion). Accuracy of 1e-7 or better is expected.

Example:

input:
2 3 2
1 -1
1 1
-1 1
1 -0.5 -0.5
-0.5 -0.5 1
3
-1 1
0.7 0.7
0.5 -0.5

answer:
-0.8949073 0.8949073 -0.41585997 -0.41585997 0.8152177 -0.8152177

Here topology 2-3-2 means we have two inputs, two outputs and single hidden layer of 3 neurons. Next 3 lines are weights for 3 neurons of the hidden layer. 1 -1 for the first, 1 1 for the second and -1 1 for the third of hidden neurons. Two more lines are weight coefficients for the output neurons: 1 -0.5 -0.5 for the first output and -0.5 -0.5 1 for the second output.

Let's check calculation manually. For the first test-case X1=-1, X2=1 the values in the hidden layer are:

H1  =  Fa(X1 * 1  +  X2 * -1)  =  Fa(-1 * 1  +  1 * -1)  =  Fa(-2)  =  -0.9640276
H2  =  Fa(X1 * 1  +  X2 * 1)   =  Fa(1 * 1  +  -1 * 1)   =  Fa(0)   =  0
H3  =  Fa(X1 * -1  +  X2 * 1)  =  Fa(-1 * -1  +  1 * 1)  =  Fa(2)   =  0.9640276

Now for output values we get:

Y1  =  Fa(-0.964 * 1  +  0 * -0.5  +  0.964 * -0.5)  =  Fa(-1.446)  =  -0.895
Y2  =  Fa(-0.964 * -0.5  +  0 * -0.5  + 0.964 * 1)   =  Fa(1.446)   =  0.895