Algae Robot - CodeAbbey

The idea to create problem about L-Systems was proposed by Sergey Pobezhimov. Problem #220 at ProjectEuler was proposed as an example. However I hope this one is far easier! :)

Enter the sequence of A and B characters and click the button

We are developing a new generation of autonomous vacuum-cleaninig robots (small and expensive devices crawling around your room and collecting dust from the corners - also useful as a toy for cats see wiki).

To simplify the design and make the thing cheaper we use such mechanics and firmware that robot can make only two types of movement:

either move straight forward by 1 foot;
or move backward simultaneously turning right - almost the same as move 1 feet back, turn 90 degrees counterclockwise and then move 1 feet back again.

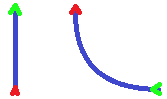
If before the step robot is placed at point 0,0 and looks forward along Y axis, then the move of the first type transfers it to the point 0,1 (preserving direction), while the move of the second type transfers it to the point 1,-1 and robot ends up looking along negative direction of X axis. Below trajectories of two types of moves are shown with red arrow depicting initial position and direction and green arrow showing final position and direction:

This manner was really used in some old remote-control toys - they moved directly forward when no receiving no signal, and started to move backward when transmitter was switched on. While moving backward their loosely fixed front wheel shifted a bit so that they also performed smooth turn.

Robot Control Program

Our robot will have several preset programs, so that customer will simply choose one of them depending on the size of the room. These programs are simply the strings of A and B characters. Letter A means the next move should be of the first type (forward) and B means the next move should be of the second type (back and turn).

Small interactive demo above allows you to try what kind of trajectories are produced by different "programs". For example, try the program AAABAAABAAABAAAB which results in a small square with four "ears" on the corners.

However we are not going to store these programs in the limited memory of our robot. Instead they are generated by the following laws:

program #0 consists of a single letter A;
each next program is generated from previous by substituting all Bs to As and all As to ABs.

Please note that substitution is performed simultaneously, so that AB generates ABA, for example. The first few programs will look therefore like these:

#0      A
#1      AB
#2      ABA
#3      ABAAB
#4      ABAABABA

This law is one of the first L-Systems proposed by Lindenmayer and is called Algae because this scientist regarded it as a model of the growth of algae - hence our robot's trade name.

Problem statement

Suppose the robot has 60 programs and is executing the last of them (#59). Also let us agree that it have started from the point 0,0 and was initially directed along Y axis.

You are given a single value - the amount of steps for which robot's battery will last. After the charge is exhausted robot stops immediately and you are to tell the position where it happened.

Input data will contain how many steps robot can perform before batteries are completely discharged.
Answer should contain X and Y of its last position.

Example:

input data:
1085555330363

answer:
-9 6