Colliding Balls - CodeAbbey

This problem is a sequel to Billiard Ball, which you are adviced to solve first!

Try to direct one of the balls to collide with another!

Now we want to play our billiard with more than one ball. So our goal is to learn processing of ball collisions.

The trick though initially puzzling, is not really that complicated.

At first let us agree that collision is 100% elastic - that is, no motion energy is spent into stable deformation of balls or dissipated as a heat. For example it means that if the ball collides with the wall it bounces back with the same speed. Or if the moving ball A hits non-moving ball B directly in the center, then A stops at once and B continues with the same speed and in the same direction.

The other helpful physical law is about the center of masses of two balls. Since the balls are of equal sizes and masses, the center of masses lays exactly between them. I.e. if coordinates of the balls are (xa,ya) and (xb,yb) then:

     xa + xb            ya + yb
xc = -------       yc = -------
        2                  2

The law we are speaking about is that despite of collision the center of masses of two balls continues moving in exactly the same direction and with exactly the same speed as it have been moving before collision.

This allows as easily switch from stationary point of view to the point of view associated with the center of mass - simply subtract the speed of the center (i.e. xc and yc) to all speeds of objects (i.e. balls) - and then add them back again.

Now, when we are looking from the center of mass we may see colliding balls and their speeds like these:

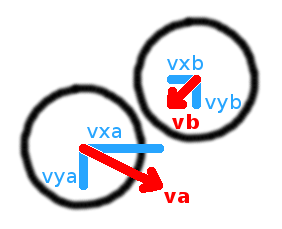
colliding billiard balls with orthogonal speeds

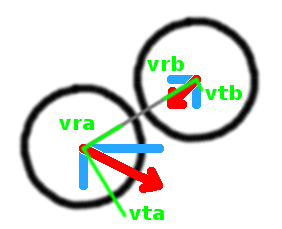
colliding billiard balls with radial and tangential speeds

You see, two balls A and B are colliding and they have velocities va and vb respectively.

The left picture shows us how these velocities are represented as the pair of coordinate-related components. Right picture instead shows us how these velocities could be represented as radial and tangential components:

radial component of the speed is that directed to the center of mass, point of collision and the center of the other ball;
tangential component is perpendicular to radial one.

These two components allow us process collision very easily:

At the moment of collision the radial component is changed to exactly opposite (i.e. turns 180 degrees), while tangential component remains unchanged.

You are welcome to create all necessary formulas yourself from this point, however if you'll find it difficult, please read step-by-step explanation at the end of this page.

Problem statement

Physics of ball moving is the same as for Billiard Ball problem. However the size of the table, balls, and deceleration value are fixed.

You are given positions and velocities of two balls - and you should track their movements for 10 seconds reporting their positions after that.

table width is 600;
table height is 300;
ball radius is 20;
deceleration constant is 5.

Input data will contain the number of test cases in the first line.
The following lines will contain 8 values each: Xa Ya Xb Yb Vxa Vya Vxb Vyb - i.e. pair of coordinates of the first ball, pair of coordinates of the second, pair of velocity components of the first ball and the same pair for velocity of the second.
Answer should give 4 values Xa Ya Xb Yb for each case after exactly 10 seconds of moving.

Since slight variations of the algorithm and numeric calculations could lead to imprecise results, your output is considered correct if any of coordinates hits in +/- 50 grace range around corresponding expected value. I.e. if you will calculate point (270, 130) instead of (250, 150) it will be OK.

Example:

input data:
4
235 124 365 176 181 34 -34 -14 
78 85 522 215 172 61 -35 -10 
221 130 379 170 183 73 -38 -10 
96 131 504 169 152 5 -30 -3

answer:
399 104 106 62 424 259 278 163 24 127 416 124 572 249 86 127

Collision in details

Your main loop may contain two main parts - moving balls and processing their collisions:

t = 0
WHILE t < 10

    FOR each ball
        moveBall(ball)
    END FOR

    FOR each pair of balls
        checkCollision(ballA, ballB)
    END FOR

    t = t + dt
END WHILE

where moveBall as earlier should consist of incrementing ball's coordinates according to speed components, and then decrementing speed components according to deceleration.

Now checkCollision(A, B) may consist of the following steps:

determine difference of coordinates of balls and distance between them:

dx = xb - xa
dy = yb - ya
d = sqrt(dx^2 + dy^2) // pythagor, ha-ha!

If the d is greater than 2 radiuses of the balls, then balls do not touch at all and we can exit this procedure.

Otherwise let us find the speed of the center of mass:

vxc = (vxa + vxb) / 2
vyc = (vya + vyb) / 2

And to switch to the reference point (point of view) linked with this center we'll find what is the speed of the ball A here:

ux = vxa - vxc
uy = vya - vyc
u = sqrt(ux^2 + uy^2)

If this speed u is too small, for example less than 1e-7 we can exit the procedure (this is optional).

Now let us find what is radial velocity of the ball A towards center of mass. To lessen the possible error we achieve this not via trigonometry but rather via dot product. Really, we only want the projection of the vector u described by components ux and uy to the vector d described by components dx and dy. Since the dot product in geometric and coordinate form looks like:

(u*d)  =  |u| * |d| * cos(u,d)  =  ux*dx + uy*dy

and projection is just the length of the vector being projected multiplied by the cosine of the angle between vectors:

ur = |u| * cos(u,d)  =  (u*d) / |d|  =  (ux*dx + uy*dy) / |d|

Now the only thing remains is to "invert" this component of the velocity. Let us "split" ur into components:

uxr = ur * dx / d
uyr = ur * dy / d

And simply subtract these components doubled from the components of the velocity of the ball A:

// va - 2*ur
vxa = vxa - 2 * uxr
vya = vya - 2 * uyr

Now what with the second ball? The nice thing is that its velocity when looking from the center of mass is just the opposite of the veolocity of the first ball (prove this by calculations!), so its radial component is also just negation and we end up with adding ur instead of subtracting it:

// vb + 2*ur
vxb = vxb + 2 * uxr
vyb = vyb + 2 * uyr

While debugging collision it is quite useful to check the following case

100 50 300 50 100 0 0 0

I.e. the first ball moves directly to the second which is not moving at all. You know, after collision the first should stop at once and the second should start moving with the same speed in the same direction.

Sample tabulation

To help you in debugging, here is the tabulation of positions of balls for the first case of the example data given above:

 t   xa  ya  xb  yb
--------------------
0.1: 253 127 362 175
0.2: 271 131 358 173
0.3: 289 134 355 172
0.4: 307 138 352 171
0.5: 323 139 350 171
0.6: 329 129 359 183
0.7: 335 120 368 194
0.8: 340 110 377 206
0.9: 346 101 385 218
1.0: 352 91 394 229
1.1: 358 82 403 241
1.2: 363 73 411 252
1.3: 369 63 420 263
1.4: 375 54 429 275
1.5: 380 45 437 274
1.6: 386 35 446 263
1.7: 391 26 454 251
1.8: 397 23 463 240
1.9: 402 32 471 229
2.0: 408 41 479 218
2.1: 413 50 488 207
2.2: 419 59 496 196
2.3: 424 68 505 185
2.4: 429 76 513 174
2.5: 435 85 521 163
2.6: 440 94 529 152
2.7: 445 103 537 141
2.8: 451 111 546 131
2.9: 456 120 554 120
3.0: 461 129 562 109
3.1: 466 137 570 98
3.2: 471 146 578 88
3.3: 477 154 574 77
3.4: 482 163 566 67
3.5: 487 171 558 56
3.6: 492 179 550 46
3.7: 497 188 542 35
3.8: 502 196 535 25
3.9: 507 204 527 26
4.0: 512 212 519 36
4.1: 517 220 511 46
4.2: 522 228 503 56
4.3: 526 236 496 67
4.4: 531 244 488 77
4.5: 536 252 480 87
4.6: 541 260 473 97
4.7: 546 268 465 107
4.8: 550 276 458 117
4.9: 555 276 450 127
5.0: 560 268 443 137
5.1: 564 261 435 147
5.2: 569 253 428 156
5.3: 574 245 420 166
5.4: 578 238 413 176
5.5: 577 230 406 186
5.6: 573 223 398 195
5.7: 568 215 391 205
5.8: 564 208 384 215
5.9: 559 201 377 224
6.0: 555 193 369 234
6.1: 550 186 362 243
6.2: 546 179 355 253
6.3: 542 172 348 262
6.4: 537 165 341 271
6.5: 533 158 334 279
6.6: 529 150 327 270
6.7: 524 143 320 261
6.8: 520 136 313 252
6.9: 516 130 306 243
7.0: 512 123 299 233
7.1: 508 116 292 224
7.2: 504 109 285 215
7.3: 499 102 279 206
7.4: 495 96 272 197
7.5: 491 89 265 188
7.6: 487 82 258 180
7.7: 483 76 252 171
7.8: 479 69 245 162
7.9: 475 63 238 153
8.0: 472 56 232 144
8.1: 468 50 225 136
8.2: 464 43 219 127
8.3: 460 37 212 119
8.4: 456 31 206 110
8.5: 452 25 199 101
8.6: 449 22 193 93
8.7: 445 28 187 85
8.8: 441 34 180 76
8.9: 437 40 174 68
9.0: 434 46 168 59
9.1: 430 52 161 51
9.2: 427 58 155 43
9.3: 423 64 149 35
9.4: 419 70 143 27
9.5: 416 75 137 22
9.6: 412 81 131 30
9.7: 409 87 125 38
9.8: 406 93 118 46
9.9: 402 98 112 54
10.0: 399 104 106 62