Теорема Пифагора

Треугольник называется прямоугольным если один из его углов прямой, равный 90° - т.е. прилежащие ему стороны перпендикулярны.

Такие треугольники важны поскольку для них действует Теорема Пифагора. Давайте, вспомним её.

Стороны, прилежащие прямому углу в таком треугольнике, называются катетами, а третья сторона - гипотенузой. Теорема утверждает, что длина гипотенузы определяется по длине катетов в соответствии с простой формулой:

c^2 = a^2 + b^2

    или

c = sqrt(a^2 + b^2)

Где c - длина гипотенузы, а длины катетов - a и b.

Известный пример прямоугольного треугольника - со сторонами находящимися в соотношении 3, 4 и 5. Действительно, для них теорема выполняется:

5^2 = 3^2 + 4^2

    или

25 = 9 + 16

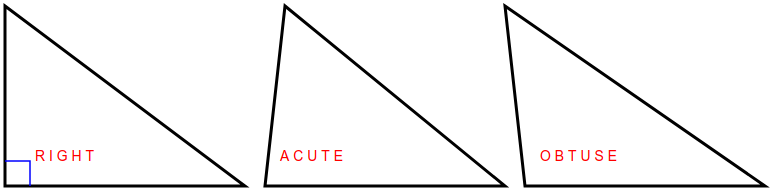
В этой задаче мы напишем программу, которая использует теорему Пифагора, чтобы определить является ли треугольник прямоугольным (right), или он остроугольный (acute), или тупоугольный (obtuse):

• в остроугольном самая длинная из сторон короче, чем должна была бы быть гипотенуза;
• в тупоугольном - наоборот длиннее.

Входные данные указывают количество тестовых треугольников в первой строке.
Остальные строки описывают по одному треугольнику каждая. Описание содержит три значения - длины сторон. Для простоты самая длинная всегда будет последней.
Ответы должны содержать одну из букв R (right), A (acute) или O (obtuse) для каждого из треугольников, через пробел.

Пример:

входные данные:
3
6 8 9
9 12 15
16 12 22

ответ:
A R O