This problem is to be solved using Turing Machine, not any general language like Python or C++
Popularly known Game of Life is an example of "cellular automaton" in 2-dimensional space. Surprisingly, even in 1-dimensional space there exist automatons which, despite very simple description, make produce fascinating patterns and even pose some yet unsolved problems.
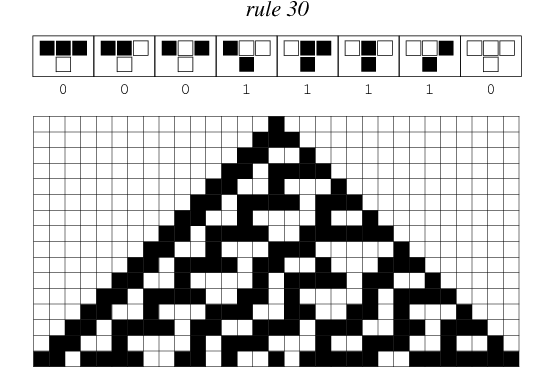
One of such automatons is known as Rule 30 - please visit a link for detailed original explanation of the name etc - below follows simplified description.
Suppose we have a 1D space (e.g. string or array, but potentially endless) filled with 0-s and 1-s. It is
updated - all cells simultaneously - according to the following rule:
Regard the current cell with its left and right neighbors. They form some 3-bit binary value. If this value
is in range 1..4 inclusive (i.e. 001, 010, 011, 100) - then current cell is set to 1 in next
generation. Otherwise it is set to 0.
Popular example is the evolution of single initial 1 (regard emptiness on right and left as endless chains of
zeroes):
step 0: 1
step 1: 1 1 1
step 2: 1 1 0 0 1
step 3: 1 1 0 1 1 1 1
step 4: 1 1 0 0 1 0 0 0 1
step 5: 1 1 0 1 1 1 1 0 1 1 1
The image at the top presents this evolution in larger number of steps.
Problem Statement
Create a program for Turing Machine which, getting sequence of 1-s and 0-s as input produces the next
state of the Rule 30 automaton. Assume sequence starts and ends with 1 (as spaces are considered zeroes,
there is no sense in leading/trailing zeroes). Assume machine starts at the left end.