Sound-Controlled Robot

Sorry for this problem may have a bit overwhelming amount of text and instructions - but this is for those not well acquainted with signal processing. However let it be :) as it shows very popular problem encountered when working with data from various sensors (either in scientific research or embedded programming etc).

The short video above presents small wheeled robot I've made some years ago to amuse students at the local school where I give electronics classes.

This robot uses small microphone to react to sounds of certain frequencies - so it can be controlled by some musical instrument (I used "recorder", e.g. a kind of flute) or even just whistling (if one has a perfect ear).

Further I shall explain briefly how it works. The current implementation is not perfect - and this problem is about improving it!

The robot has small electronics control board (on the top of central column, to reduce noise from motors) which bears the microphone, microcontroller chip (one of the smallest ARMs with 1k RAM) and few simple components to connect all this stuff (resistors, capacitors, amplifier and LED).

Microcontroller uses built-in analog-to-digital converter (ADC) to measure signal from microphone 8000 times per second. This gives a stream of values in range 0 .. 255. Vibrations of sound produce oscillating changes in these values.

If the sound produces plain sine-like waveform, we can easily calculate period of this sine wave by measuring distance between tops or crosses with average. And thus calculate frequency (which is f = 1/T where T one period duration).

However in reality sound is not a sine wave, it includes some overtones, some random noise - and even probably some low-frequency (e.g. 50Hz) interference from nearby equipment.

So microcontroller uses digital filters to get rid of these unwanted "additions". The picture below shows typical noisy input sequence (in blue) and the output from the filter (in red).

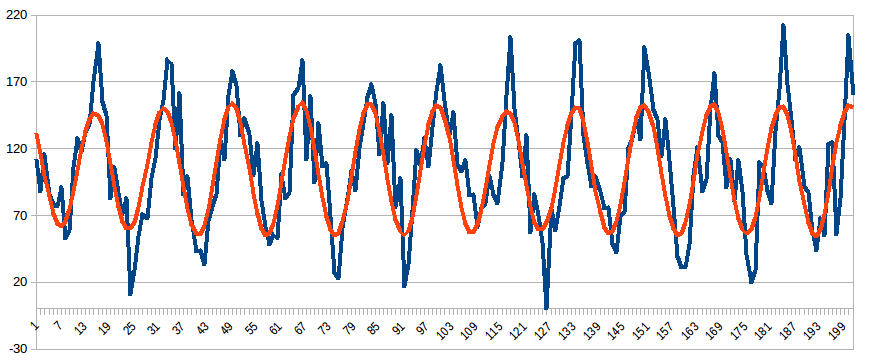
We can easily judge the waveform "by sight", however precise analysis (especially by microcontroller which has no "sight") becomes feasible only with filtering. Filter is really just a simple math formula, which leaves "wanted" sine-like components intact and reduces others.

Now, what is wrong with my robot? It uses several filters (e.g. several formulas) tuned to frequencies of several notes and then tries to compare their outputs to detect which note is being played. This approach appeared somewhat complicated and imperfect. So let's try to create an improved version.

Let's agree that new version of robot will react to sounds of several close frequencies (i.e. with difference only of 5 Hz) so that we can use single filter for all of them. After filtering let's try to detect the frequency, for example, by counting crosses with zero. The drawback is that we probably won't be able to control it with musical instrument anymore (musical notes are not so close), but we can make dedicated sound producing device for this purpose.

So what is our task

The robot should be able to distinguish 7 "command" frequencies with the step of 5 Hz, e.g. 400, 405, ... 430.

Input data will contain sequence of 7 such commands chosen randomly. Each command is being played for about 37.5 milliseconds (i.e. 300 samples of robot's ADC, see above), followed by 12.5 millisecond pause (100 samples).

And we want to know, which frequencies were played. So to solve the problem we probably want:

• implement digital filter (you may refer to this instruction and use BPF)
• create some frequency calculating algorithm for sine-like wave
• bind this all together

Input data will have 2 values in the first line - smallest and highest of command frequencies - this may help in tuining your filter. Frequencies are somewhere around 440 Hz. Samples sequence is split to multiple lines just for convenience - make sure to read it whole.

Next lines contain samples, as recorded from ADC - i.e. integers in range 0 .. 255 amounting to 7 commands with 6 spaces between them.

Answer should give 7 values - frequencies of the commands we have detected from the input sequence.

Example:

input:
410 440
27 128 114 107 109 138 182 139 188 116 79 ...

answer:
440 420 425 420 425 420 420